Commutative algebra in mixed characteristic
(a conference in honor of Bhargav Bhatt's Rowlee Lecture)

The University of Nebraska-Lincoln Math department will host a conference on Saturday, March 29, 2025, in Lincoln, Nebraska. This is a sister event to the 2025 Rowlee Lecture, which will be given by Bhargav Bhatt on Friday, March 28.
- Alessandro De Stefani (University of Genova)
- Jakub Witaszek (Princeton University)
- Linquan Ma (Purdue University)
- Anurag K. Singh (University of Utah)
Application:
Register here to attend the conference and to apply for funding. We have limited funding to cover travel expenses, so priority will be given to early-career participants. We ask all attendees to register by March 24, 2025; the deadline to apply for travel funding is January 24, 2025.
Schedule:
Participants should plan to arrive before 3 pm on March 28. The conference will end at 3 pm on Saturday, March 29.
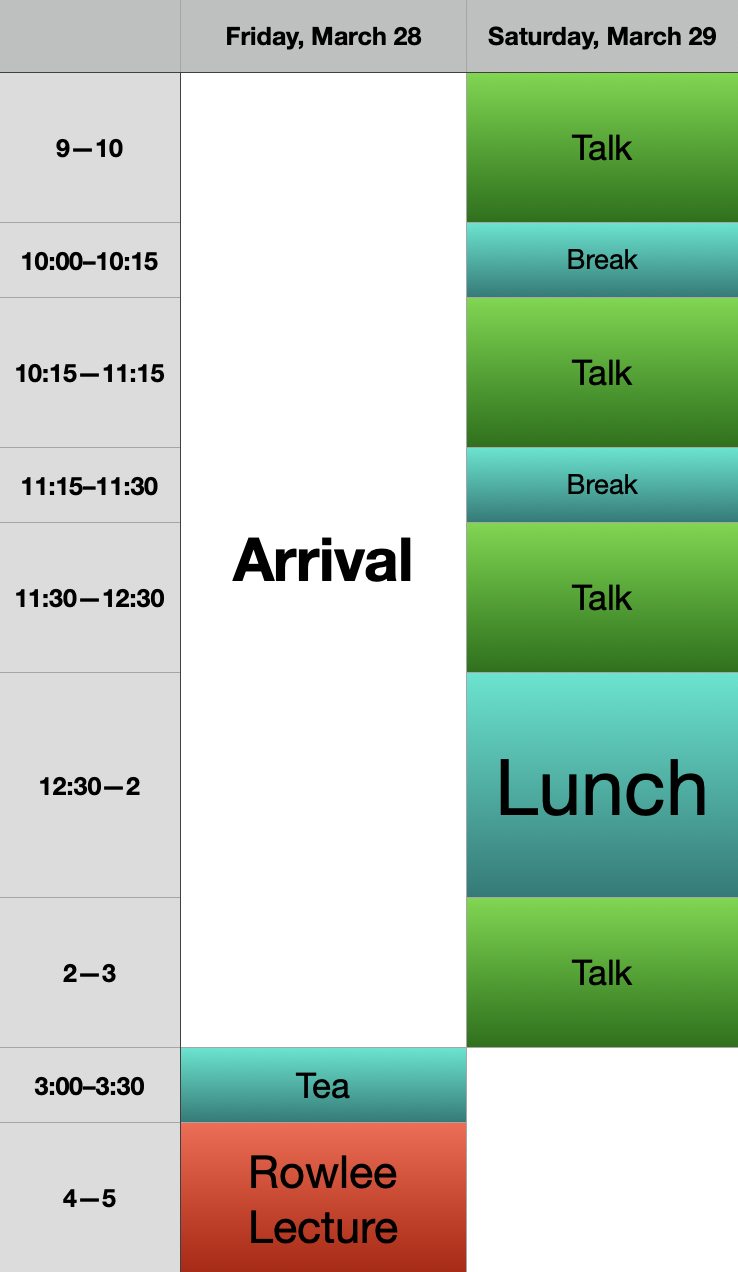
All talks will be held in Avery 115.
Abstracts:
Bhargav Bhatt (Institute for Advanced Study and Princeton University)
The p-adic numbers: past and present
Abstract: For each prime number p, there is a number system — the p-adic number system — rather analogous to the standard (real) number system. This system was discovered in the late 1800s and has played a vital role in many areas of mathematics. The past 15 years have witnessed some major breakthroughs in our understanding of geometries built from this number system; this has had downstream effects, such as the solution of longstanding problems across a variety of fields. In this talk, I will first explain what the p-adic number system is and then give a high-level overview of some of the new ideas that led to the recent developments.
Alessandro De Stefani (University of Genova, Italy)
Connectedness of the associated graded ring
Abstract: In this talk we will discuss how certain connectedness properties of a complete local ring R descend to its associated graded ring G. The main tool we use is a homogenization technique which produces a complete "Gröbner-like" deformation of R with special fibre the completion of G. The cases of equal and mixed characteristic need to be treated separately: we will discuss similarities and differences. Time permitting, we will also discuss some consequences of these results on certain numerical invariants of R. This talk is based on joint work with Maria Evelina Rossi and Matteo Varbaro.
Linquan Ma (Purdue University)
Perfectoid pure singularities
Abstract: We introduce a mixed characteristic analog of F-pure singularities, which we call perfectoid pure singularities. We will present some basic and expected properties of these singularities and show their connections with log canonical and Du Bois singularities. We will discuss some examples and many related open questions. This talk is based on joint work with Bhargav Bhatt, Zsolt Patakfalvi, Karl Schwede, Kevin Tucker, Joe Waldron, and Jakub Witaszek.
Jakub Witaszek (Princeton University)
Hodge Theory of Singularities in Positive Characteristic
Abstract: I will start by reviewing various Hodge-theoretic invariants of complex singularities. After that, I will discuss an approach to interpreting these invariants using methods from positive characteristic. This is based on joint work with Tatsuro Kawakami.
Anurag K. Singh (University of Utah)
Are determinantal rings pure subrings of polynomial rings?
Abstract: Let G be a linearly reductive group over a field K, with a linear action on a polynomial ring over K. Then the invariant ring is a pure subring of the polynomial ring; many key properties of classical invariant rings of characteristic zero, as in the Hochster-Roberts theorem or in Boutot's theorem, follow from purity. The classical invariant rings that we primarily have in mind here are determinantal rings, symmetric determinantal rings, and rings defined by pfaffians. It is natural to ask whether, in the case of positive characteristic, these are pure subrings of polynomial rings. This remains largely unresolved, though positive answers would be very useful. It turns out that the analogous question over the rings of integers or over the ring of p-adic integers can be answered completely; this is joint work with Jack Jeffries.
Travel information:
The University of Nebraska-Lincoln is located in Lincoln, Nebraska. If you live within driving distance, we strongly encourage you to drive to Lincoln. If you need to fly, there is an airport in Lincoln, and the Omaha airport is about an hour away by car. The Oma-Link shuttle provides transportation between the Omaha airport and Lincoln, but it is unfortunately quite expensive. An one way uber costs typically around $100; we might be able to cover a few uber rides to and from the Omaha airport, but only if there is a group of participants sharing it. We strongly encourage participants to fly to Lincoln instead.

